Example 13.12: Equilibrium Concentrations in a Solution of a Weak Acid
Formic acid, \(\ce{HCO2H}\), is the irritant that causes the body’s reaction to ant stings ( Figure 12).
Figure 12: The pain of an ant’s sting is caused by formic acid. (credit: John Tann)
What is the concentration of hydronium ion and the pH in a 0.534-M solution of formic acid?
\(\ce{HCO2H(aq)}\)\(\ce{ + }\)\(\ce{H2O(l)}\)\(\ce{<=>}\)\(\ce{H3O+(aq)}\)\(\ce{ + }\)\(\ce{HCO2-(aq)}\)\(\ce{ }\)
Solution
\(K_{\mathrm{a}}\) \(= 1.8\times 10^{-4}\)\([\ce{HCO2H}]_{\mathrm{init}}\) \(= 0.534\)
Determine x and equilibrium concentrations. The equilibrium expression is:
\(K_{\mathrm{a}} = \dfrac{[\ce{H3O+}]_{\mathrm{eq}} \cdot [\ce{HCO2-}]_{\mathrm{eq}}}{[\ce{HCO2H}]_{\mathrm{eq}}}\)
The concentration of water does not appear in the expression for the equilibrium constant, so we do not need to consider its change in concentration when setting up the \(\ce{ICE}\) table.
The table shows initial concentrations (concentrations before the acid ionizes), changes in concentration, and equilibrium concentrations follows (the data given in the problem appear in color):
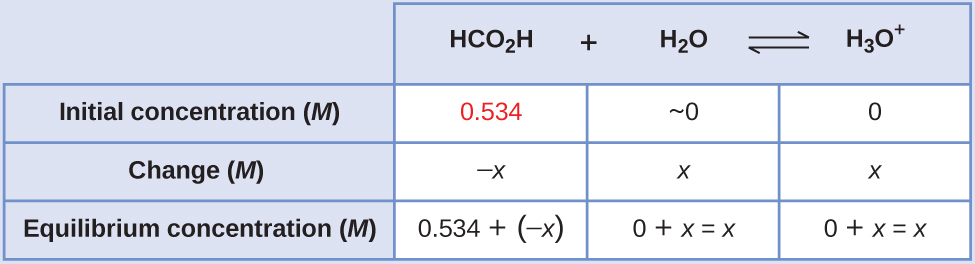
Solve for x and the equilibrium concentrations. At equilibrium:
\(K_{\mathrm{a}} = \dfrac{[\ce{H3O+}] \cdot [\ce{HCO2-}]}{[\ce{HCO2H}]} = \dfrac{x \cdot x}{[\ce{HCO2H}]_{\mathrm{init}} - x}\)
Because the initial concentration of acid is reasonably large and \(K_{\mathrm{a}}\) is very small, we assume that x << [HCO2H]init, which permits us to simplify the denominator term \(\mathrm{as} \cdot ([\ce{HCO2H}]_{\mathrm{init}} - x) = [\ce{HCO2H}]_{\mathrm{init}}\) This gives:.
\(K_{\mathrm{a}} = \dfrac{{x}^{2}}{[\ce{HCO2H}]_{\mathrm{init}}}\)
Now solve for x as follows:
\([\ce{HCO2H}]_{\mathrm{init}} \cdot K_{\mathrm{a}} = {x}^{2}\)
\(x = \sqrt{K_{\mathrm{a}} \cdot [\ce{HCO2H}]_{\mathrm{init}}}\)
\(x\) \(= \sqrt{K_{\mathrm{a}} \cdot [\ce{HCO2H}]_{\mathrm{init}}}\)
\(\ \ \ =\sqrt{1.8\times 10^{-4} \cdot 0.534}\)
\(\ \ \ =\sqrt{9.61\times 10^{-5}}\)
\(\ \ \ =9.8\times 10^{-3}\)
To check the assumption that x is small compared to 0.534, we calculate the ratio and express it in percent:
\(\mathrm{ratio}\) \(= \dfrac{x}{0.534} \cdot 100\ \mathrm{％}\)
\(\ \ \ =\dfrac{9.8\times 10^{-3}}{0.534} \cdot 100\ \mathrm{％}\)
\(\ \ \ =0.01836 \cdot 100\ \mathrm{％}\)
\(\ \ \ =1.84\ \mathrm{％}\)
x is less than 5% of the initial concentration; the assumption is valid.
We find the equilibrium concentration of hydronium ion in this formic acid solution from its initial concentration and the change in that concentration as indicated in the last line of the table:
\([\ce{H3O+}]_{\mathrm{eq}}\) \(= 0 + x\)
\(\ \ \ =0 + 9.8\times 10^{-3}\)
\(\ \ \ =9.8\times 10^{-3}\)
The pH of the solution can be found by taking the negative log of the [H3O+], so:
\(\mathrm{pH}\) \(= -\mathrm{log}([\ce{H3O+}]_{\mathrm{eq}})\)
\(\ \ \ =-\mathrm{log}(9.8\times 10^{-3})\)
\(\ \ \ =2.01\)